フーリエ変換 メモ2 -フーリエ変換の変数の意味と使用例-
【3】フーリエ変換の変数
どの言語でも対応できるようにしたいので実際のコードではなく、あくまで具体的な利用法を文章で記述していきます
まず現実の音データを受け取ったものを f(x) とします
前回のフーリエ変換の定義式の f(x) に対応しています
さて、前回ディリクレの条件を満たすあらゆる関数はsin波とcos波の足し合わせで出来ていることを説明しました
これは受け取る音データに関しても言えることです。ちなみにある関数をsin波とcos波の足し合わせで表現できる形に直すことをフーリエ変換といいます。
これから受け取ったデータをフーリエ変換しよう、つまり「sin波とcos波で表現しよう」というのですから、そのデータはディリクレの条件を満たしていると仮定して進めていくことになります
というか基本的に無視しても問題ないと思います
前回の定義式は

でした
音に関しては f (x)のxは時間経過で増えていくサンプルの数になります
例えばサンプリングレートが44100Hz(1秒間に44100回サンプルを取る)で一秒間録音した場合
一番最初のサンプルの値はf(0 ) 、一番最後のものはf (44099)に入っています
ここで定義式の中の変数の具体的な意味を見ていきましょう
まずは2πですこれは言わずもがな、360度であり、円です
次にN、これは周期です
周期で2πを割るということは1周期で丁度1回転しますね
Σで変化させている x は2π/Nを0から2πギリギリまで変化させています
周期の単位は「秒」ですからxは時間による変化を示す変数と言えます
では t は何を示す変数なのでしょうか
t = 1のときのcos と sin の中身について考えて見ましょう
t = 1のときのcos と sin の中身は共に 2πx/N
先ほども説明したとおり x は 2π/Nを0から2πギリギリまで変化させます
要するに t = 1のときは丁度周期Nで一周する周波数のフーリエ変換と言えます
この波形を示すとこうなります

では次にtを2にした波形を示します

横軸の長さは変わらす繰り返しの回数が増えましたね?
ではt=3のときは?もう画像を貼らなくても分かりますね?繰り返しの回数は3回になります
そう、t は周波数を制御する変数といえます
こと音に関して言えばフーリエ変換とは
時間の関数を周波数の関数に写像する変換
ということができます
では周波数 t はどこからどこまでの範囲にすればいいの?
という話になりますね
私の経験則で申し訳ないのですが音データのサンプル数/2まで移動させれば大丈夫です
もし不十分な場合は音データのサンプル数と同じHz(サンプル数が10000なら10000Hz)まで移動させれば確実です
以上までがフーリエ変換の詳しい話です
【4】フーリエ変換の具体的な使用法
いよいよもって具体的な利用法です
といっても[3]で殆ど説明してしまったのでまとめるだけになります
虚数を格納する変数 image と実数を格納する変数 real を用意します
変数 k を1ずつ増やして、音データ数の半分になるまでループ
{
real (k) = 0で初期化
image (k) = 0で初期化
変数 t を 周期-1 まで1ずつ増やしてループする
{
real ( k ) = real ( k ) + real ( t ) * cos(2πtx / N)
imag( k ) = imag( k ) + image( t ) * sin(2πtx / N)
}
}
こんな形になります
ね?簡単でしょ?
#初稿2015年4月1日
フーリエ変換 メモ1 -フーリエ変換の発想と離散フーリエ変換-
音に関するプログラムをいろいろ組んでみたので忘れないうちにここにメモして置きます
※正しいとは限りません御了承ください
フーリエ変換について
第一にフーリエ変換とは与えられた関数の構成要素を調べる数式です
定義式は

となります
π:円周率
i :虚数
しかしこれをコンピュータ上で行う場合∞というのは扱いに困りますし、これだけ与えられても具体的にどう取り扱っていいのか分かりませんよね?少なくとも私は分かりませんでした。
よって以下に私が分かればいいや程度で説明していきます。
【1】そもそもフーリエ変換の基本的な発想は?
(まとめだけ読んでもたぶん差し支えありません)
そもそもの始まりは「あらゆる関数はsin波とcos波の足し合わせで表現できる」ということをフーリエさんが発見したことでした(流れは違うかもしれませんが基本的なアイディアはこれです)sin波とcos波の足し合わせで表現する関数をフーリエ級数と呼びます。
フーリエさんの「あらゆる関数はsin波とcos波の足し合わせで表現できる」という考え、
実際にはあらゆる関数に適応させることは出来ませんでした
フーリエさんの考えを適応するためには条件があったのです
その条件はディリクレの条件と呼ばれています
といってもディリクレの条件はゆるく、殆どの関数が条件を満たします。唯一注意する必要のありそうな条件は
「周期的な関数でなくてはならない」というものです
周期的といっても大抵の関数は周期的と呼ぶには些か不規則です
ですがこう見るとどうでしょう
ここに全く周期的でない波形があります

上の波形が周期的に繰り返される関数だと考えると

ね?周期的でしょう?
非周期的な関数でも同じものが後に繰り返されていると考えると良いです
こうして考えるとあらゆる関数は周期的であるということができます
<まとめ>
・ディリクレの条件を満たすあらゆる関数はsin波とcos波での足し合わせで表現できる
・ディリクレの条件は非常にゆるい
【2】コンピュータ上でのフーリエ変換の利用
さて、前項に「ディリクレの条件を満たすあらゆる関数はsin波とcos波での足し合わせで表現できる」 と書いているのに最初に提示されたフーリエ変換にcosもsinもないじゃないか!と思う人もいるでしょう
フーリエ変換の∞の扱いどうするんだ!という疑問と共に答えていきます
まずコンピュータ上では∞を厳密に扱えないため、離散フーリエ変換(略称DFT)を扱います
以下が定義式です

N:任意の整数(周期をいれる変数)
i :虚数
π:円周率
というわけで∞は消えました
Σの意味はいいですね?
xが0からN-1までxの値を変化させながらΣの中の物を足していくという意味です
このままsin波とcos波を出していきます
ここにオイラーの公式があります


となりsinとcosが出てきました
離散フーリエ変換の定義式がsin波とcos波の足し合わせで表現されていることが理解できましたか?
f(x)はいいの?という声もあるかもしれませんがsinとcosの係数なので問題ないです
虚数を扱えるプログラミング言語では離散フーリエ変換の定義式をそのまま使えば問題はありません
しかし扱えないプログラミング言語の場合は最後に示したフーリエ変換のsinとcosの状態から実数と虚数で分けて計算しなくてはいけません
プログラムでの具体的な使い方は長くなってきたのでまた今度
#初稿2015年4月1日
AA自動作成ツール(ひとまずりりーす)
前回の記事で別の手法を試すと言ったな
あれは嘘だ
正直いうともうちょっとでなんとかなりそうな気がしたので頑張ってた。
前回までのはMSゴシックの文字をビットマップで読み込んでいた。
これは等幅フォントと呼ばれていて横幅も縦幅も全ての文字で一致している。
だからもうこっちの方でサイズを指定しちゃえばよくね?と思い至った。
その結果がこれ

ちょっと縦に潰れちゃってるけど大体わかる。
潰れてる部分は今後の課題、二値化の部分の精度がわるいこともあって今はこんなところ。
もっと簡単な画像だともうすこしだけ綺麗になる。

右端になんか出てるのはたぶん二値化のせい
そのうちgithubにあげる
githubにあげた
AA自動作成ツール(途中)
前回AA作成ツールを修正すると書き、この記事を書くまで試行錯誤をしていた。
今回はその中身を書いていく
前回までのはC言語で作成していた。AA化のアルゴリズム自体に不備は無かったんだけど画像を読み込むときとか十分に大きく取った配列に画像を読み込むとかいう変なことをしてたので可変長配列を扱いやすいC++で書き直した。
それで書き直すついでにアルゴリズムの手順ひとつひとつを関数化してどこが問題になってるか原因をわかりやすくした。
特定できた原因は
・GetGlyphOutline関数
これだ。
これは与えた文字のビットマップを返してくれるwin32apiで用意されている関数なんだけど結構いろんな記事でバグがー、罠がーといわれている。私も例に漏れずかかってしまった。
帰ってくる処理結果は以下のような図になる。
GetGlyphOutline関数のフォント位置 様より勝手に参照

gmCellIncXが文字の空白も含んだXのサイズで
gmBlackBoxXが空白を含まないXのサイズ
gmGlyphOrigin.xがgmCellIncX上での文字の起点のX座標だ
この理解が間違えてなければgmCellIncX >= gmBlackBoxXは常に成り立つはずだ
これがまず変になってしまう
jをGetGlyphOutline関数に与えると
gmCellIncX >= gmBlackBoxXの関係が崩れる
というかgmGlyphOrigin.xなんか負の値が帰ってくる
ためつすがめつ見てみると以下の関係が見えてきた
gmCellIncX = gmBlackBoxX + gmGlyphOrigin.x
どのような文字をGetGlyphOutlineに与えようとこの関係だけは不変だった
文字の横幅のサイズが保証されなくなってしまったために上記の横幅を示す3要素をいじって試すかしかなくなってしまった
とりあえず試したのが上の等式を変形したこの形
gmBlackBoxX = gmGlyphOrigin.x - gmCellIncX
上の画像の関係が割りと怪しくなってるのでその関係を持ち出すのは正直意味無いと思うが他にリファレンスもないので頼ると横幅のサイズはgmBlackBoxXよりも小さくはならないのでまぁやってみる

知ってた(白目)
他にも手がないし・・・ってことで gmCellIncXだけを横幅として試してもみたがダメだった。
後ちょっとで出来そうな気もするがちょっと仕様がよくわからんようなものを使ってたく無いので別の手法で試します。
AA自動作成ツールを作る(みかん)
3年前にAAを自動で作成するツールを作ってバグバグなまま放置してたので腰を据えて作ろうと思う
その時に考えてた基本的なアルゴリズムが以下
1.画像を読み込む
2.画像を微分
3.フォントサイズを指定(文字で幅が変わらない等幅フォントとする)して画像を分割
4.文字のビット列を取得
5.分割した画像それぞれと複数の文字のビット列を比較して最も一致率の高かったものを出力する
win32APIのgetGlyphOutlineで文字のビット列を受け取っていたのですが正直面倒というか・・・
win32APIはあんまり使いたくないのでもっと便利なものがあれば使いたい
一応2年前の状態を張って置く
1と2にあたる部分が以下の画像
左が画像の読み込み部、右が微分して出力した画像
4にあたるのが以下の画像
これは「おやすみ」のビット列を読み込んで適当な文字に置き換えて出力している
上記二つを組み合わせて処理を行った結果が以下
下のが元画像
左がAAとして出力したもの 右が画像のビットマップを0と1で出力したもの
フォントサイズは2である
AAのほうはこんな小さいフォントなら文字とか関係なく元画像と同じように見えるに決まってるだろっていう突っ込みはさておき、画像右側に行くにつれて元画像との違いが出ている
バグだ
続いてフォントサイズ12で作ったもの
もうだめ
とりあえず今後の目標としては
・このブレを直す
・処理が重いので軽量化を目指す
の2点と締めくくっていた
なのでこれから頑張る
processingでとことんぷよぷよを作成した
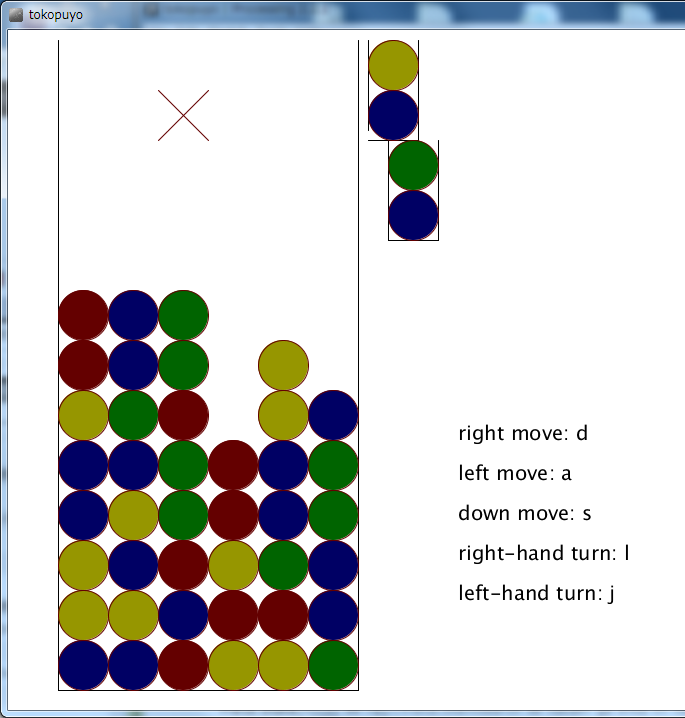
processingにて「とことんぷよぷよ」を作成した
上の画像がそれ
実装期間は4日程、何気に時間を使ったのは回転処理とか。コードの4分の1は回転とかのキー操作でなんとか短くしたい
githubにコードを載せたけど正直書いたのが前過ぎてあんまり覚えてないしコードが汚い
もし良かったら遊んでみて欲しい
プラットフォームを作ったので将来的にぷよぷよAIとかもつくってみたいかも